Comparing probabilistic search and linear search methods

In my last post I did a little comparison of behaviors between the linear search and binary search algorithms. Not surprisingly, the binary search algorithm makes fewer iterations than the linear search, regardless of the list size. There, I mentioned that while the binary search is very effective for ordered data, it may not find the correct values in unsorted lists. My conclusion was that only a probabilistic algorithm could maybe have a chance of beating the linear search method. In this post I will show briefly that a simple probabilistic algorithm may not beat, unfortunately, the linear search method for unordered lists.

Comparison of algorithms

The following linear search algorithm is similar to the one I showed in my previous post: it starts in the top of the list and goes through all its elements until it find the wanted value.

def linear_search(value, list):
    """
    Returns the index of a value in the list.

    """

    for index, val in enumerate(list):
        if value == val:
            return index

    return None

The probabilistic search method is a also a very simple algorithm: it continues to generate random index positions until it finds the desired value.

def prob_search(value, l):
    """
    Returns the index of a value in a list
    using a probabilistic search.

    """

    indexes = list(range(len(l)))
    random.shuffle(indexes)

    for index in indexes:
        if l[index] == value:
            return index

    return None

To compare the two methods I used an approach similar to the one in my previous post: each algorithm was adapted to return the number of iterations, and for each list of each size, both algorithms were run 100 times and their average number of iterations calculated. The source code can be found in this gist.

The following figure shows the average number of iterations of each algorithm for lists sizes from 10 to 1000.

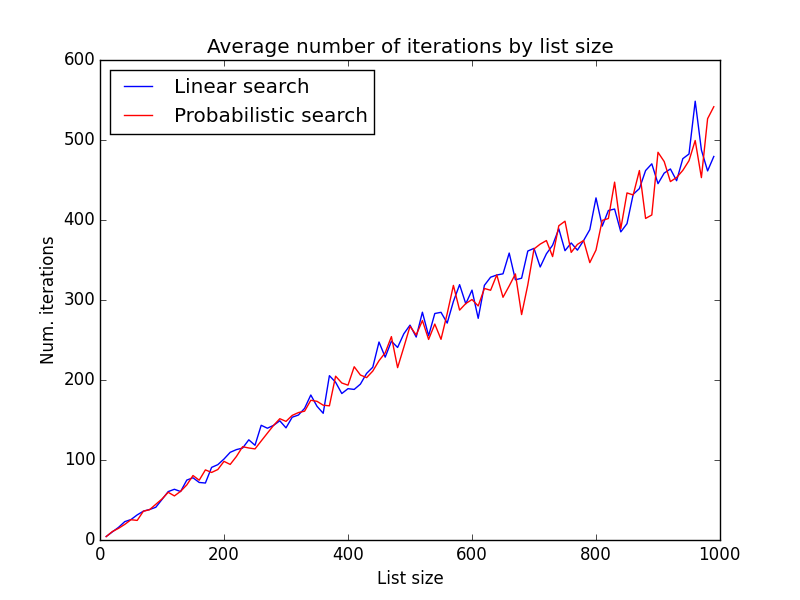
As shown, both methods have similar behavior independently of the list size. Perhaps changing the random number generator distribution could change slightly the results, but I'm not so sure. It will stay as future work!