The Sierpinski triangle

The Sierpinski triangle is a fractal with the form of a triangle subdivided recursively into smaller ones. This wikipedia page talks about it in some detail and shows several different ways of building the triangle. In this post I will show an implementation using the chaos game technique.

The chaos game technique works as follows:

1. Create a n x n grid and find 3 points that form a triangle.
2. Randomly choose an initial vertex.
3. Randomly select one of the vertices.
4. Compute the half distance between your current point and the selected vertex.
5. Plot the current position
6. Go back to step 3.

Here's a very simple Python implementation that uses matplotlib:

import random
import matplotlib.pyplot as plt


def plot(points):
    """
    Plots the points using matplotlib.
    Points is a list of (x, y) pairs.
    """

    xx = [x for (x, y) in points]
    yy = [y for (x, y) in points]

    plt.plot(xx, yy, 'g.')
    plt.show()


def sierpinski(n):
    """
    Generates positions for the Chaos Game Sierpinski
    triangle with 'n iterations in a square of size 1x1.
    """

    vertices = [(0.0, 0.0), (0.5, 1.0), (1.0, 0.0)]
    points = []

    # initial vertex
    x, y = random.choice(vertices)

    for i in range(n):
        # select new vertex
        vx, vy = random.choice(vertices)

        # get middle point
        x = (vx + x) / 2.0
        y = (vy + y) / 2.0

        points.append((x, y))

    plot(points)


sierpinski(n=1000)

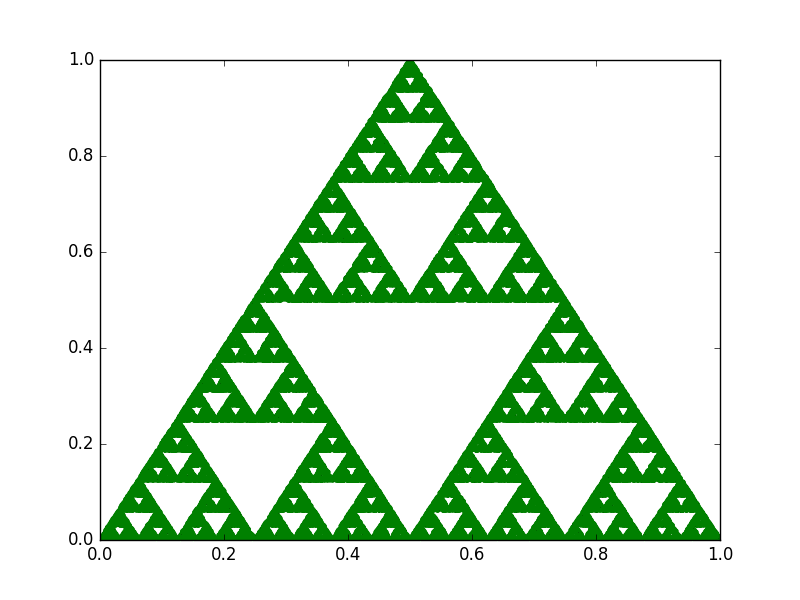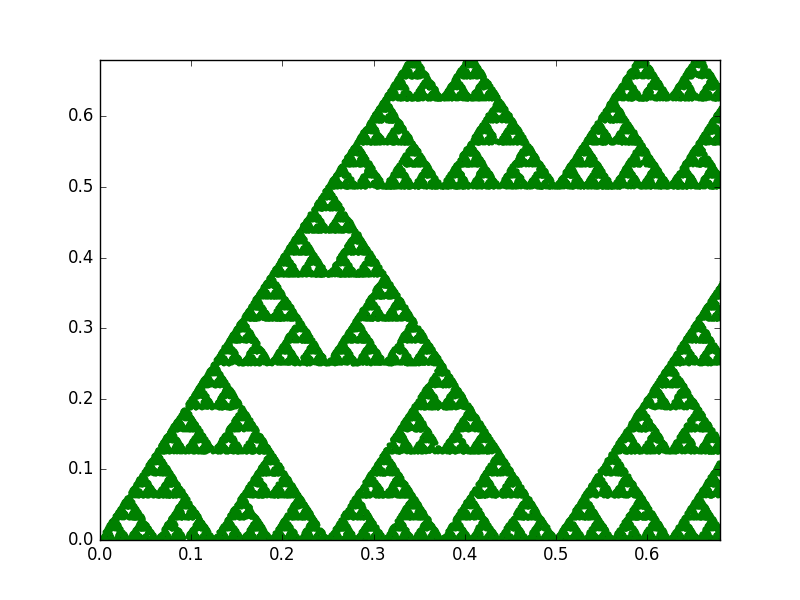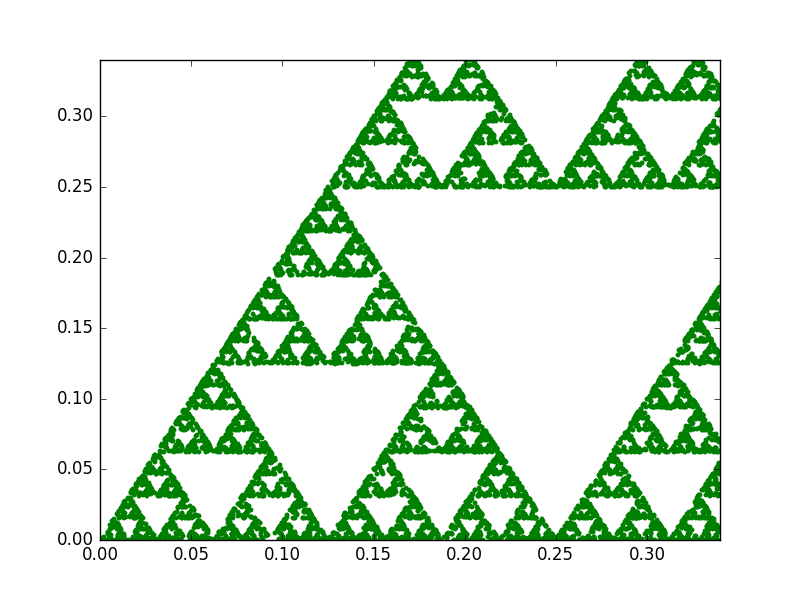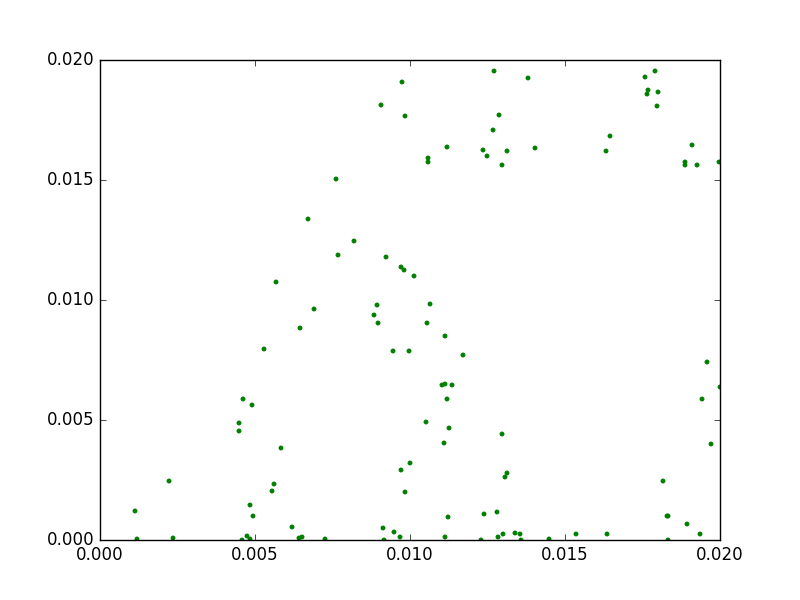
And here's how the triangle looks after a specific number of iterations:

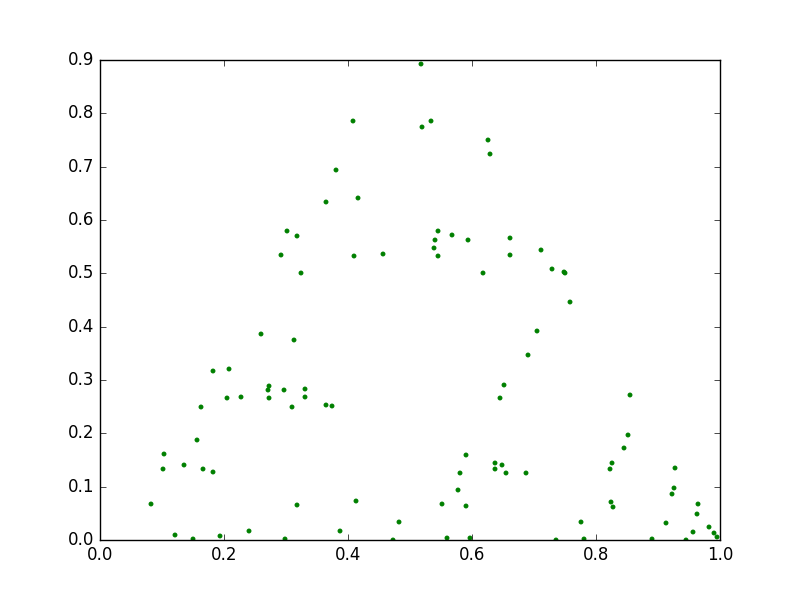
100 iterations

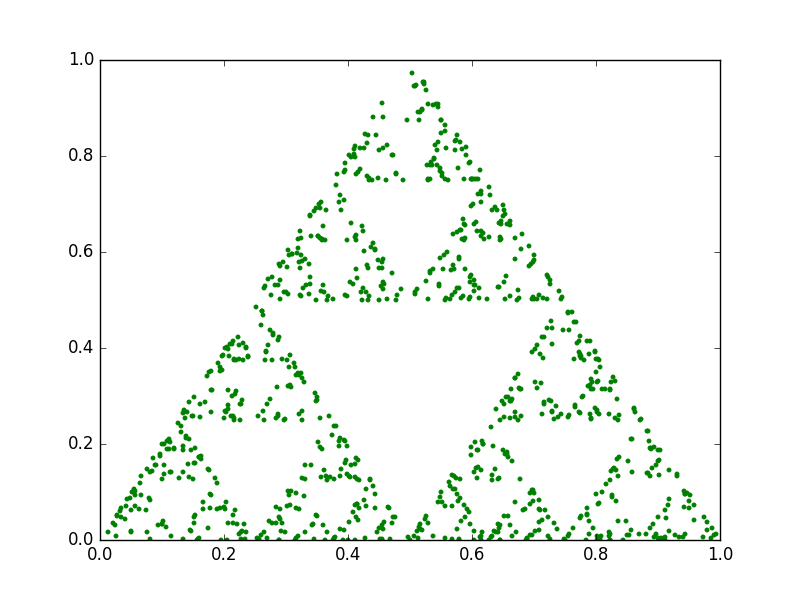
1.000 iterations

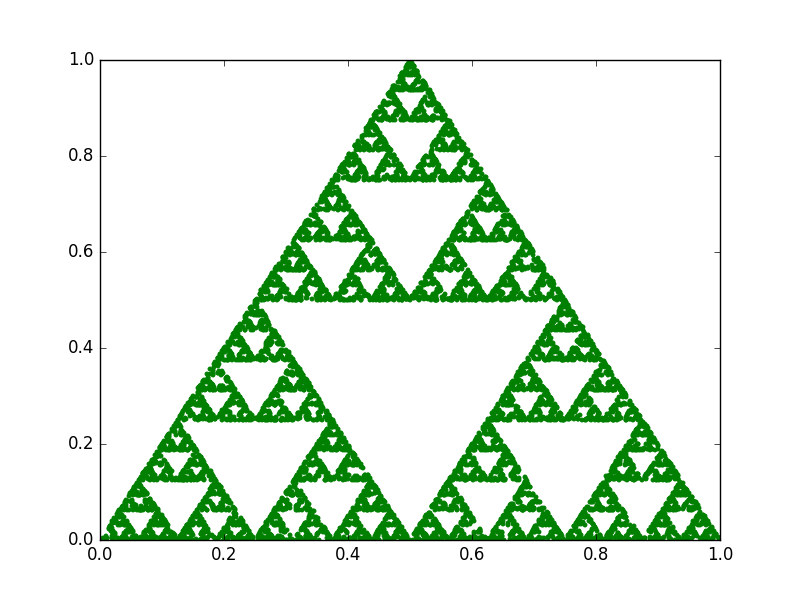
10.000 iterations

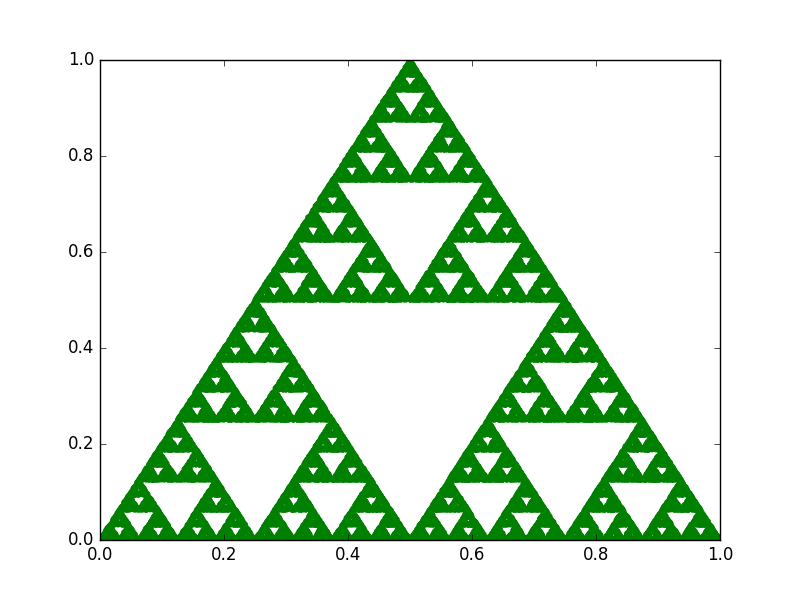
50.000 iterations

An interesting property of fractals is that they exhibit a repeating pattern that displays at every scale. In other words, they are infinitely scalable. However, with the chaos game technique, if we do not find a way to recompute the points every time we increase the zoom level, eventually we will start noticing them. For instance, check this animation between two triangles with 1.000 and 50.000 points:

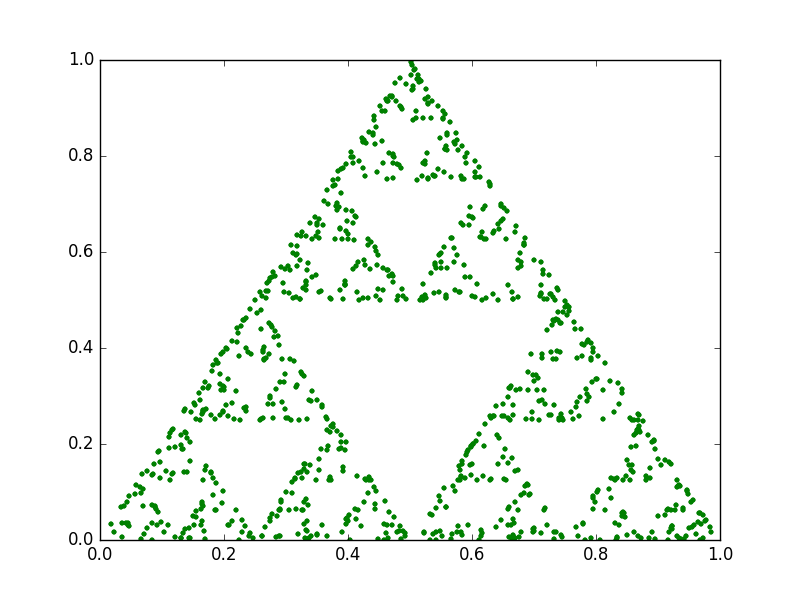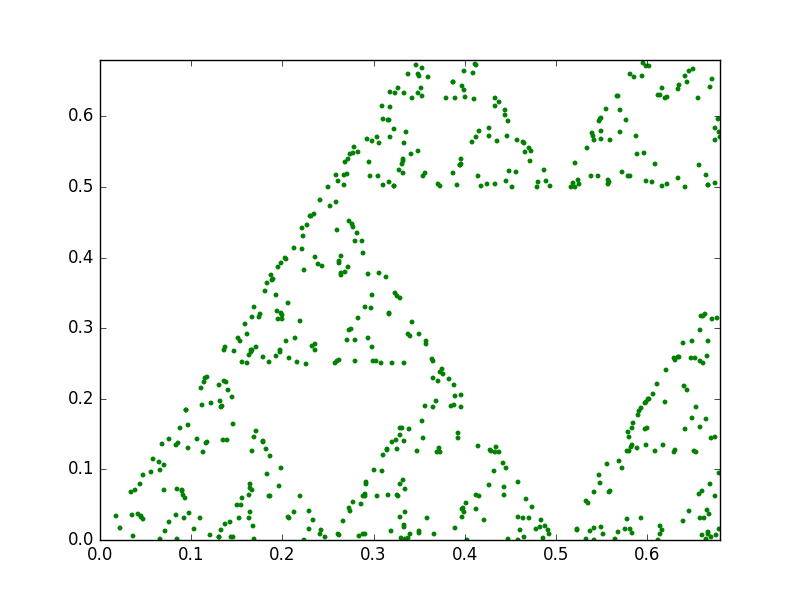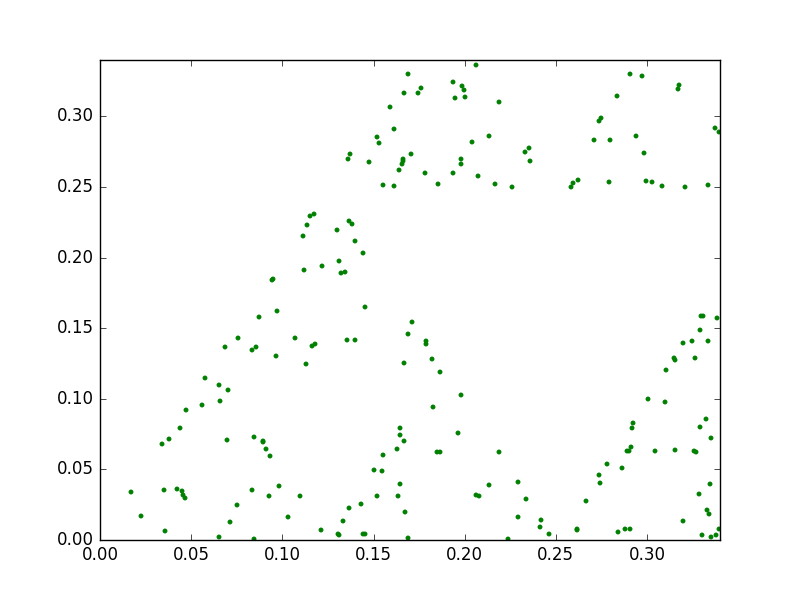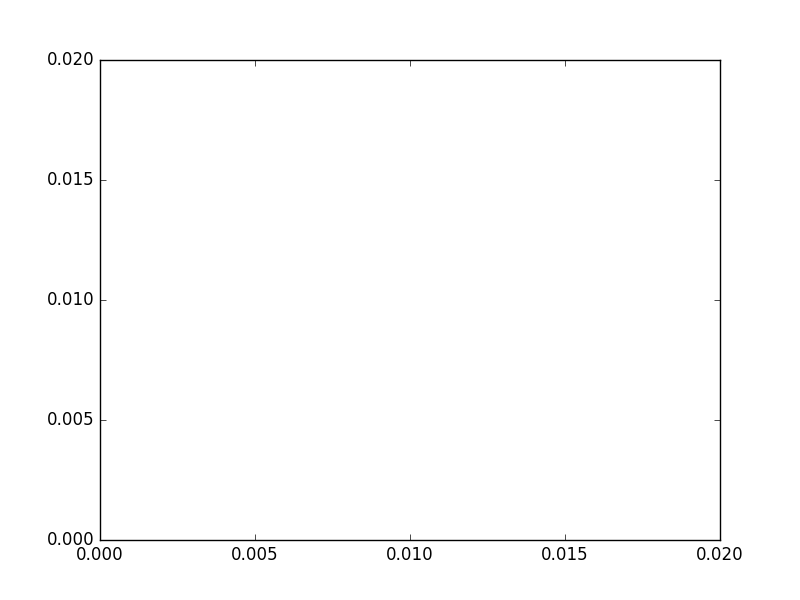
1.000 points

50.000 points

The entire source code for the Sierpinski Triangle (with the animations) can be found in this gist.